José | org | 12. 4. 2024 21:49:55
Hola hej, hola hou!
Hintíky už k tobě jdou! :D
3. jarní série
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
3. seriálová série
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Hintíky už k tobě jdou! :D
3. jarní série
Úloha 1. + skrytý text
Prostě to udělej! ;)
Úloha 2. + skrytý text
Párů je 151, což je jen kousek od 150.
Úloha 3. + skrytý text
Áďa to dokáže. + skrytý text
Když uděláš z čísel dost velkou ohrádku, vejdou se všechna i dovnitř.
Úloha 4. + skrytý text
Odhadni, kolik může být duplicit mezi kartami. + skrytý text
Pro konstrukci začni s úplným grafem, symboly nechť jsou hrany. To ale nebude úplně stačit.
Úloha 5. + skrytý text
Uvaž matfyzáka, který tančil s nejvíce matfyzačkami. + skrytý text
A pak matfyzačku, která s ním netančila.
Úloha 6. + skrytý text
Zkus si lidi představit jako vrcholy grafu s hranami dvou barev (jedna barva odpovídá Kecalovu plánu, druhá Kecalčině). Jak tento graf vypadá (resp. jak vypadají jeho souvislé komponenty)?
Úloha 7. + skrytý text
Všimni si, že 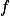 a
a 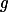 musí být bijekce.
musí být bijekce.
Úloha 8. + skrytý text
Co kdyby Klárka nejdříve chtěla získat alespoň tolik pravých rukavic jako levých... + skrytý text
a ve správnou chvíli strategii změnila?
3. seriálová série
Úloha 1. + skrytý text
Pomocí poměrů spočítej body 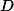 a
a 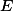 . Pak pomocí vzorečků a podobností počítej jednotlivé přímky.
. Pak pomocí vzorečků a podobností počítej jednotlivé přímky.
Úloha 2. + skrytý text
Ze seriálu víme, že platí 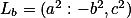 ,
, 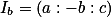 . Průsečík přímek pak už dokážeš snadno spočítat.
. Průsečík přímek pak už dokážeš snadno spočítat.
Úloha 3. + skrytý text
Je-li 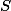 průsečík
průsečík 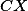 a
a 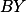 , zajistíš rovnoběžnost tak, že
, zajistíš rovnoběžnost tak, že 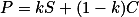 a
a 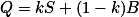 . Zvol si souřadnice bodů
. Zvol si souřadnice bodů  ,
,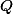 ,
,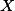 ,
,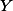 co nejjednodušeji. + skrytý text
co nejjednodušeji. + skrytý text
Chordálu získáš jako rozdíl rovnic kružnic. Pro důkaz, že přímky prochází jedním bodem, spočítej determinant.
Denisa Hanušková | org | 6. 3. 2024 08:57:39
Ahoj, nová várka hintů je zde, s nimi hravě dořešíš úlohy 2. jarní série.
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
Úloha 1.+ skrytý text
23. účastník je kamarád všech, takže i 1. účastníka.
Úloha 2.+ skrytý text
Umísti kamarády k prostřednímu sloupu.
Úloha 3.+ skrytý text
Uvaž největší místnost v libovolných dvou po sobě jdoucích kolech.
Úloha 4.+ skrytý text
Stačí ukázat, že kamarád průsečíku leží na výšce z  .
.
Úloha 5.+ skrytý text
Všichni moji přátelé se přátelí navzájem.
Úloha 6.+ skrytý text
Najdi švrčkův bod
Úloha 7.+ skrytý text
Překlop 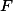 podle stran.
podle stran.
Úloha 8.+ skrytý text
Ukaž, že 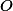 a
a 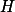 jsou kamarádi v čtyřúhelníku
jsou kamarádi v čtyřúhelníku 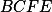 , tudíž
, tudíž 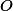 leží na ose
leží na ose 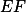 .
.
José | org | 7. 2. 2024 15:21:21
Za týden je svátek zamilovaných. A kdo by nemiloval hinty 1j a 2s série ;).
1. jarní série
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
2. seriálová série
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
1. jarní série
Úloha 1. + skrytý text
Zkus napsat spoustu trojiček se součtem 6.
Úloha 2. + skrytý text
Všimni si, že nsn si od každého prvočísla vybere tu největší vyskytující se mocninu.
Úloha 3. + skrytý text
Znaménko rozdílu se může změnit nanejvýš jednou.
Úloha 4. + skrytý text
Najdi prosté zobrazení z počtu způsobů pro n do počtu způsobů pro n+1.
Úloha 5. + skrytý text
Dívej se na racionální čísla modulo 5.
Úloha 6. + skrytý text
Posviť si na posloupnost bn = √(an+1 + an).
Úloha 7. + skrytý text
Fn je Fibonacciho číslo, Gn je od jistého okamžiku rozdíl dvou Fibonacciho posloupností.
Úloha 8. + skrytý text
Celočíselné body na hyperbole x^2 - 2cxy + y^2 + c^2 - 1 = 0.
2. seriálová série
Úloha 1. + skrytý text
Použij vzorce pro otáčení (vrcholy čtverců nad stranami) a pro rovnoběžník.
Úloha 2. + skrytý text
Vzorec ortocentra trojúhelníka na jednotkové kružnici máš, |a-b| = √((a-b)(a-b)). + skrytý text
Pozn. (a-b) zde značí číslo komplexně sdružené.
Pak si jen vzpomeň na vzorce:
.ζk = ζ7-k,
ζ7+k = ζk.
.ζk = ζ7-k,
ζ7+k = ζk.
Pozn. (a-b) zde značí číslo komplexně sdružené.
Úloha 3. + skrytý text
Vepsaná kružnice je jednotková, vzorec na průsečík tečny s tětivou máš. To nejhorší se pokrátí.
José | org | 13. 1. 2024 07:17:51
Due to technical difficulties, we are currently unable to post mathematical text in this chat, forcing us to post this next series of hints as plain text. We hope to get the issue resolved soon, so that we can post a more readable version in the near future. We apologize for the inconvenience.
Problem 1. + skrytý text
Problem 2. + skrytý text
Problem 3. + skrytý text
Problem 4. + skrytý text
Problem 5. + skrytý text
Problem 6. + skrytý text
Problem 7. + skrytý text
Problem 8. + skrytý text
Problem 1. + skrytý text
Pigs eat more food than chickens.
Problem 2. + skrytý text
Square it, then arrange it into a square.
Problem 3. + skrytý text
Show that any triangle placed completely inside a unit square has an area of at most 1/2.
Problem 4. + skrytý text
Divide out what you can, you will be left with a product of |m-n|/2 bigger numbers vs a product of |m-n|/2 smaller numbers.
Problem 5. + skrytý text
Use the AM-GM inequality.
Problem 6. + skrytý text
For each divisor d, calculate how many times it will be counted in the sum. + skrytý text
Get a bound on the sum using floor(n/d) - floor(n/(d+1)) >= 0.
Problem 7. + skrytý text
Square the given recurrence relations. + skrytý text
You only need to show (x_n)^2 + (y_n)^2 + (z_n)^2 > 6n+39.
Problem 8. + skrytý text
Use the sum formula. + skrytý text
And apply Cauchy–Schwarz.
Denisa Hanušková | org | 6. 12. 2023 21:47:20
Netrpělivě očekáváš hinty z 3. podzimní série a 1. seriálové série? Zde jsou:
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 1. + skrytý text
Pythagorův trojúhelník.
Úloha 2. + skrytý text
Lze to. + skrytý text
Minimální počet kružnic je 6. + skrytý text
Existuje konfigurace se dvěma různými poloměry kružnic.
Úloha 3. + skrytý text
Ukažte, že poloměry kružnic tvoří geometrickou posloupnost.
Úloha 4. + skrytý text
Dokaž, že A, B, S, T a střed 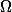 leží na jedné kružnici.
leží na jedné kružnici.
Úloha 5. + skrytý text
Překlop podle 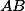 . Srovnej velikosti kružnic.
. Srovnej velikosti kružnic.
Úloha 6. + skrytý text
Dokaž, že součet úhlů 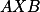 ,
, 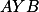 a
a 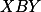 je 180 stupňů.
je 180 stupňů.
Úloha 7. + skrytý text
Nejdřív vyúhli kolmost stran+ skrytý text
vzdálenost protějších přímek spočti dokreslením tětiv 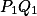 ,
, 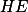 ,
, 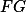 a společné tečny
a společné tečny 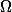 ,
, 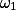 v bodě
v bodě 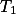 .
.
Úloha 8. + skrytý text
Střed strany 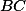 leží na pevné kružnici, stejnolehli ho na těžiště a Feuerbašiště.+ skrytý text
leží na pevné kružnici, stejnolehli ho na těžiště a Feuerbašiště.+ skrytý text
Podruhé stejnolehli pevnou kružnici z opsiště, je pevné. Poloměr Feuerbachovy kružnice taky znáš.
Úloha 1.+ skrytý text
Obsah trojúhelníka a sinová věta.
Úloha 2.+ skrytý text
Hýbej bodem  . Když
. Když 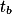 značí délku tečny z
značí délku tečny z  k
k 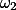 , je
, je 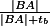 konstanta.
konstanta.
Úloha 3.+ skrytý text
Najdi tu kružnici a prostě to spočítej. Co by se mohlo pokazit?
José | org | 17. 11. 2023 17:53:23
Stále bádáš nad nějakou úlohou z 2. podzimní série? Další hinty už ti spěchají na pomoc!
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Smaž čtvereček na levé hraně.
Úloha 2. + skrytý text
Jsou-li 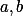 nesoudělná, co musí platit aby
nesoudělná, co musí platit aby 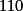 dělilo
dělilo 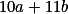 ?
?
Úloha 3. + skrytý text
Rozmysli si, jak se ciferné součty mění při přechodu přes desítky a že aspoň 20 po sobě jdoucích čísel nepřejde přes stovky.
Úloha 4. + skrytý text
Ukaž, že je to součet lichých čísel menších než 2n.
Úloha 5. + skrytý text
Najít množinu 2n-1 obdélníků je snadné, zkus potom nějaký přidat. + skrytý text
Setřiď velikosti stran 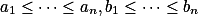 . BÚNO
. BÚNO 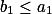 , najdi
, najdi 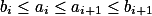 .
.
Úloha 6. + skrytý text
Musí mít všechny stejný zbytek po dělení p. Počítejte s polynomy těch čísel a jejich kořeny modulo p.
Úloha 7. + skrytý text
Stačí čtyři díly. Čtverec 5x5 vyřízne v celku. + skrytý text
Schodiště je výhodný řez, díly se dají posunout o jeden schod a zase spojit.
Úloha 8. + skrytý text
Indukuj podle k. + skrytý text
Dokazuj kombinatoricky: kolika způsoby lze 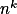 lidí rozdělit do
lidí rozdělit do  -tic?
-tic?
Denisa Hanušková | org | 8. 10. 2023 22:15:55
Ahoj, trápíš se stále s nějakou úlohou z 1. podzimní série? Hinty Ti pomohou vydat se správným směrem.
Úloha 1. + skrytý text
Úloha 2.+ skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Trojúhelníky AEB a ACB mají společnou výšku.
Úloha 2.+ skrytý text
Cesta se nemá kde zacyklit.+ skrytý text
Začneme v 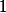 , kde je vůbec možné skončit?
, kde je vůbec možné skončit?
Úloha 3. + skrytý text
Může. Jaké znáš Pythagorejské trojice?
Úloha 4. + skrytý text
Vietovy vztahy
Úloha 5. + skrytý text
Nakreslete si graf množství vody v dromedárově hrbu v závislosti na čase. Předpokládejte, že voda nedojde.
Úloha 6. + skrytý text
Zakresli si mrakodrapy do grafu, kde hrana bude mezi mrakodrapy, pokud je rozdíl jejich výšek mocnina dvou.
+ skrytý text
+ skrytý text
Když v grafu necháme každou mocninu dvou pouze jednou, musí být acyklický.
Úloha 7. + skrytý text
Nakreslete si do n-úhelníka obdélníky tvaru (délka strany) x  .
.
Úloha 8. + skrytý text
Odpověď je 2. Podívej se na stát s nejmenším počtem základen. + skrytý text
Pro základnu patřící jinému státu vezmi nejkratší část pobřeží, který dostáváš ze zadání.
Áďa | org | 24. 5. 2023 16:41:55
Vrtá Ti stále hlavou nějaká úložka z finálního myšmaše? Pak zde jsou hinty právě pro Tebe!
Úloha 1.
a) + skrytý text
b) + skrytý text
Úloha 2.
a) + skrytý text
b) + skrytý text
Úloha 3.
a)+ skrytý text
b)+ skrytý text
Úloha 4.
a)+ skrytý text
b)+ skrytý text
Úloha 5.
a)+ skrytý text
b)+ skrytý text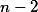 zakroužkovaných lze docílit -- najdi konstrukci.+ skrytý text
zakroužkovaných lze docílit -- najdi konstrukci.+ skrytý text
Úloha 6.
a)+ skrytý text
b)+ skrytý text
Úloha 7.
a)+ skrytý text
b)+ skrytý text
Úloha 1.
a) + skrytý text
Zkus přepnout jednu žárovku na obvodu, aniž bys změnil stav jiných.
b) + skrytý text
Dokresli průsečíky výšek trojúhelníků 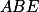 a
a 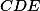 .
.
Úloha 2.
a) + skrytý text
Rozmysli si, který bod musí být růžový, aby v dalším kroku byl obarvený střed. Pak ukaž, že tak daleko růžový bod nikdy nebude.
b) + skrytý text
Najdi potenční střed 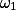 ,
, 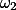 a
a 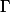 .
.
Úloha 3.
a)+ skrytý text
Rozlož rozdíl čtverců.+ skrytý text
modulo 4
b)+ skrytý text
Posloupnost nemůže růst velkými skoky.+ skrytý text
Najdi dost dlouhý úsek složených čísel.
Úloha 4.
a)+ skrytý text
Rozeber součty 3, 4, 5, 6 a 12, 13, 14, 15.
b)+ skrytý text
Osoba s největším počtem známostí v rámci jedné skupiny.
Úloha 5.
a)+ skrytý text
Podmínky s celočíselnými průměry vyřeší množina plná násobků 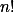 .+ skrytý text
.+ skrytý text
Nesoudělnosti docílíš posunutím.
b)+ skrytý text
K důkazu, že 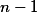 dosáhnout nelze, uvažuj vrchol s nejmenším stupněm a potom ten s druhým nejmenším.
dosáhnout nelze, uvažuj vrchol s nejmenším stupněm a potom ten s druhým nejmenším.
Úloha 6.
a)+ skrytý text
Omez shora hodnotu tohoto zlomku. Tato hodnota musí dělit číslo tvaru 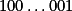 , které má o cifru víc než
, které má o cifru víc než  .
.
b)+ skrytý text
Dokresli rovnoběžku k 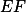 skrz
skrz  .
.
Úloha 7.
a)+ skrytý text
Podívej se na hodnoty 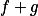 .
.
b)+ skrytý text
Uvaž 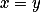 a
a 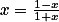 .
.
Denisa Hanušková | org | 6. 4. 2023 21:24:19
Ahoj! Skončili nám další série a hinty se hlásí o slovo.
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text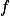 je prostá a
je prostá a 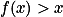 .+ skrytý text
.+ skrytý text
Úloha 8. + skrytý text
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 1. + skrytý text
Dej všem funkcím 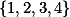 a cyklicky je vůči sobě posuň.
a cyklicky je vůči sobě posuň.
Úloha 2. + skrytý text
Uspořádej kořeny do dvojic, které jsou osově souměrné podle 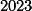 .
.
Úloha 3. + skrytý text
Použij dolní celou část. Jak se chová na záporných číslech?
Úloha 4. + skrytý text
Použij Vietovy vztahy pro zadané kvadratické trojčleny.
Úloha 5. + skrytý text
Získej nějaké  splňující
splňující 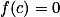 a dosaď ho za
a dosaď ho za 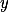 .
.
Úloha 6. + skrytý text
Dosazením 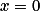 uvidíš, co se děje na nezáporných číslech.
uvidíš, co se děje na nezáporných číslech.
Úloha 7. + skrytý text
Prohoď  a
a 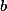 .
.
Úloha 8. + skrytý text
Označme 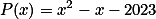 , jaké jsou hodnoty
, jaké jsou hodnoty 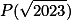 a
a 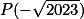 ?+ skrytý text
?+ skrytý text
Uvaž pevné body 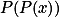 .+ skrytý text
.+ skrytý text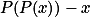 je polynom čtvrtého stupně, nemůže tedy mít více než 4 kořeny. Má
je polynom čtvrtého stupně, nemůže tedy mít více než 4 kořeny. Má 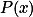 nějaké pevné body?
nějaké pevné body?
Úloha 1.+ skrytý text
Existuje třeba pro 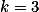 .
.
+ skrytý text
+ skrytý text
Skoro cokoli jiného než pravidelný šestiúhelník bude fungovat.
Úloha 2.+ skrytý text
Rozmysli si, proč to platí pro rovinné nakreslení.+ skrytý text
Zkus odebrat nějakou hranu tak, aby se levá strana nerovnosti zvětšila.+ skrytý text
Odeber hranu e, pro kterou je cr(e) největší.
Úloha 3.+ skrytý text
Postupuj podobně jako v posledních příkladech v seriálu.+ skrytý text
Když zafixuješ dva vrcholy trojúhelníku, množina bodů v rovině, kde by mohl být ten třetí, je elipsa.
Áďa | org | 10. 3. 2023 00:17:12
Ahoj, ahoj! Stále si lámeš hlavu nad některou z úložek 2. jarní série? Pak je tu další várka hintů právě pro Tebe!
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4.+ skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Podívej se na 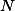 modulo
modulo 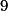 a
a 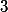 .
.
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Pro horní odhad posčítej všechny obvody dohromady a zjisti, co dostaneš v obrázku. + skrytý text
Pro dolní odhad se podívej na čtyřúhelníček v rohu ohrádky.
Úloha 4.+ skrytý text
Roznásob a substituuj 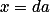 ,
, 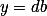 , kde
, kde 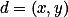 .
.
Úloha 5. + skrytý text
Nakresli si z PraSátka přímky rovnoběžné s diagonálami čtverce.
Úloha 6. + skrytý text
Protni přímky 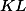 a
a 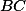 a hledej rovnoramenné trojúhelníky.
a hledej rovnoramenné trojúhelníky.
Úloha 7. + skrytý text
Uvaž funkci 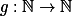 takovou, že
takovou, že 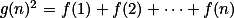 , a zkus na ni získat nějaké odhady. + skrytý text
, a zkus na ni získat nějaké odhady. + skrytý text
Rozeber hodnoty 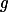 v prvočíslech.+ skrytý text
v prvočíslech.+ skrytý text
Domysli, že to už vynucuje všechny hodnoty.
Úloha 8. + skrytý text
Vyjde to 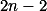 . Zobecni konstrukci pro
. Zobecni konstrukci pro 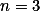 . Zafixuj počet svislých a vodorovných segmentů.
. Zafixuj počet svislých a vodorovných segmentů.
Denisa Hanušková | org | 8. 2. 2023 17:39:30
Ahoj, s koncem serií se k Vám blíží další hinty. Zde jsou:
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 1.+ skrytý text
Dívej se na rozdíly sousedních průměrů.
Úloha 2.+ skrytý text
Popáruj dělitele 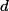 s
s 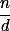 .
.
Úloha 3.+ skrytý text
Zprůměruj první a třetí nejvyšší a redukuj postupně dolů. Pro číslo 1000 opakuj postup z obou stran.
Úloha 4.+ skrytý text
Popáruj podmnožiny, které obsahují svůj aritmetický průměr s těmi, který jej neobsahují.
Úloha 5.+ skrytý text
Rozděl čísla na sudá a lichá.
Úloha 6.+ skrytý text
Spočítej 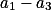
Úloha 7.+ skrytý text
Rozmysli si, že 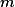 se nezvětšuje.
se nezvětšuje.
Úloha 8.+ skrytý text
Více, než 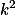 jich být nemůže, takže každá trojice, která může být pěkná, musí.+ skrytý text
jich být nemůže, takže každá trojice, která může být pěkná, musí.+ skrytý text
Uspořádej si reálná čísla podle velikosti. Podívej se na vzdálenosti 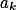 a
a 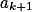 . Jak pak musí vypadat ostatní mezery?
. Jak pak musí vypadat ostatní mezery?
Úloha 1. + skrytý text
Fíla skutečně mohl takovou množinu najít.+ skrytý text
Zkus nějakou množinu bez okraje.
Úloha 2. + skrytý text
Postupně přidávej body z konvexního obalu, když to je potřeba, tak dva najednou.+ skrytý text
Přidávej body tak, aby poslední dvě písmena napsaného textu byla stejná.
Úloha 3. + skrytý text
Uvaž libovolný bod na povrchu mnohostěnu a zobraz mnohostěn ve stejnolehlosti se středem v tomto bodě a koeficientem 3/4.+ skrytý text
Použij nekonečnou Hellyho větu.+ skrytý text
Libovolné 4 obrazy se protínají v těžišti příslušného čtyřstěnu.
Áďa | org | 10. 1. 2023 11:17:38
Ahojky, už určitě netrpělivě očekáváš hintíky 4. podzimní série. Mám pro Tebe dobrou zprávu! Už nemusíš čekat déle!
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
Úloha 7. + skrytý text
Úloha 8. + skrytý text
Úloha 1. + skrytý text
Jaké dvojice můžou vzniknout při prvním rozdělení? A při druhém?
Úloha 2. + skrytý text
Čtvrté číslo zvol co nejvyšší.
Úloha 3. + skrytý text
Za jak dlouho alespoň někdo ví vše?
Úloha 4. + skrytý text
Jak musí vypadat graf, kde je mezi dvěma týmy hrana, právě když spolu hrály v některém z prvních dvou dnů?
Úloha 5. + skrytý text
Ukaž, že pokud je 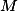 město, do kterého doletí nejvíc letadel, a
město, do kterého doletí nejvíc letadel, a  ,
,  nějaká jiná města, ze kterých letí letadla do
nějaká jiná města, ze kterých letí letadla do 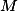 , pak úhel
, pak úhel 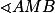 musí být vyšší než
musí být vyšší než 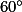 .
.
Úloha 6. + skrytý text
Smaž právě jednu šipku mezi každými dvěma týmy. + skrytý text
Rozděl si to na dvojice, kde pokaždé vyhrál jiný tým, a na ty zbylé.
Úloha 7. + skrytý text
Využij faktu, že počet přijatých GIFů je stejný jako počet odeslaných, k dokázání 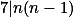 . Najdi konstrukci pro vyhovující
. Najdi konstrukci pro vyhovující 
Úloha 8. + skrytý text
Indukcí. Rozděl si maximální kliky podle toho, jak vznikly z menšího grafu.
Zdeněk Pezlar | org | 29. 12. 2022 19:27:13
Ahoj,
chceš trochu potrénovat před blížícím se krajským kolem Matematické olympiády A? Potom je tu právě pro tebe TRiKSko -- tréninková online soutěž semináře iKS. Bližší informace najdeš na https://iksko.org/triks/current.php.
chceš trochu potrénovat před blížícím se krajským kolem Matematické olympiády A? Potom je tu právě pro tebe TRiKSko -- tréninková online soutěž semináře iKS. Bližší informace najdeš na https://iksko.org/triks/current.php.
Denisa Hanušková | org | 6. 12. 2022 20:37:09
Ahoj, stále se trápíš nad některou z úloh? Pak Tě jistě potěší pozdní dárek od Mikuláše, který Ti u nás v podobě hintů zanechal.
Úloha 1. + skrytý text
Úloha 2. + skrytý text
Úloha 3. + skrytý text
Úloha 4. + skrytý text
Úloha 5. + skrytý text
Úloha 6. + skrytý text
+ skrytý text
Úloha 7. + skrytý text
+ skrytý text
Úloha 8. + skrytý text
+ skrytý text
Úloha 1.+ skrytý text
+ skrytý text
Úloha 2. + skrytý text
+ skrytý text
Úloha 3. + skrytý text
+ skrytý text
Úloha 1. + skrytý text
Vypiš si, jaká prvočísla spolu mohou sousedit.
Úloha 2. + skrytý text
Zvol za  postupně
postupně 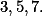
Úloha 3. + skrytý text
Pokrať 19, rozlož na součin.
Úloha 4. + skrytý text
Podívej se na paritu.
Úloha 5. + skrytý text
V posloupnosti 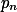 se od nějaké chvíle bude opakovat
se od nějaké chvíle bude opakovat 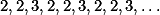
Úloha 6. + skrytý text
Označ si ony čtverce 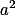 a
a 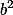 ,pak odečti a faktorizuj.
,pak odečti a faktorizuj.
+ skrytý text
Odhadni 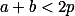
Úloha 7. + skrytý text
Faktorizuj 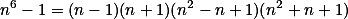
+ skrytý text
Vyjádři 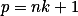 , dosaď a rozeber případy podle toho, kterou závorku
, dosaď a rozeber případy podle toho, kterou závorku  dělí.
dělí.
Úloha 8. + skrytý text
Přepiš na součin kombinačních čísel.
+ skrytý text
Přidej k součinům  , abys dostal kombinační čísla s
, abys dostal kombinační čísla s 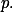
Úloha 1.+ skrytý text
Nemusí.
+ skrytý text
Protipříklad je i na čtyřech vrcholech.
Úloha 2. + skrytý text
Extremální princip.
+ skrytý text
Dívej se na úhly.
Úloha 3. + skrytý text
Udělej strom na triangulaci.
+ skrytý text
Hledej vrchol, co je "uprostřed".
Zdeněk Pezlar | org | 22. 11. 2022 13:06:52
Ahoj!
Již tradiční internetová soutěž Mathrace (http://brkos.math.muni.cz/mathrace/)
proběhne už za týden v úterý 30.11.! Soutěž je určena pro nejvýše čtyřčlenné týmy středoškoláků, pro nadšence mimo střední školu je tu kategorie Underground. Soutěž organizují studenti Přf MUNI.
Čím se liší Mathrace od jiných matematických soutěží? Na řešení úloh jsou povolené libovolné zdroje - kalkulačky, Geogebra, WolframAlpha, programování - můžete si proto být jistí, že i s pomocí těchto nástrojů budete muset nad úlohami přemýšlet.
Soutěž probíhá online, nemusíte se svým týmem sejít na jednom místě. Týmy ale musí pocházet z jedné školy.
Tak na co čekáš, registruj se na Mathrace!
Již tradiční internetová soutěž Mathrace (http://brkos.math.muni.cz/mathrace/)
proběhne už za týden v úterý 30.11.! Soutěž je určena pro nejvýše čtyřčlenné týmy středoškoláků, pro nadšence mimo střední školu je tu kategorie Underground. Soutěž organizují studenti Přf MUNI.
Čím se liší Mathrace od jiných matematických soutěží? Na řešení úloh jsou povolené libovolné zdroje - kalkulačky, Geogebra, WolframAlpha, programování - můžete si proto být jistí, že i s pomocí těchto nástrojů budete muset nad úlohami přemýšlet.
Soutěž probíhá online, nemusíte se svým týmem sejít na jednom místě. Týmy ale musí pocházet z jedné školy.
Tak na co čekáš, registruj se na Mathrace!
Áďa | org | 15. 11. 2022 12:46:01
Ahoj! Druhá podzimní série je za námi. Pokud si s nějakým příkladem marně lámeš hlavu, níže si můžeš prohlédnout hinty, které Ti pomůžou vydat se správným směrem.
Úloha 1.+ skrytý text
Úloha 2.+ skrytý text
Úloha 3.+ skrytý text
Úloha 4.+ skrytý text
Úloha 5.+ skrytý text
Úloha 6.+ skrytý text
Úloha 7.+ skrytý text
Úloha 8.+ skrytý text + skrytý text
+ skrytý text
Úloha 1.+ skrytý text
Popáruj si vzdálenosti, aby se sečetly na 9
Úloha 2.+ skrytý text
Dokresli čtverec, jehož úhlopříčka je 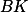 .
.
Úloha 3.+ skrytý text
Parita (sudost/lichost)
Úloha 4.+ skrytý text
Ukaž, že chatrč může být kdekoli mezi 1011. a 1012. hruškou.
Úloha 5.+ skrytý text
Dokresli si průsečíky úhlopříček zadaných obdélníků. Pomocí nich dokaž, že 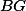 je rovnoběžná s
je rovnoběžná s 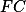 .
.
Úloha 6.+ skrytý text
Buďte 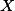 ,
, 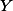 středy
středy 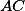 ,
, 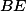 ; potom ukaž, že
; potom ukaž, že 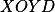 je rovnoběžník.
je rovnoběžník.
Úloha 7.+ skrytý text
Dokažte tětivovost 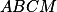 a
a 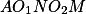
Úloha 8.+ skrytý text
Chordála Feuerbachovy kružnice a kružnice opsané
Michal Janík | 19. 7. 2022 22:29:35
Řešení 15:
+ skrytý text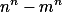 můžeme zapsat jako
můžeme zapsat jako 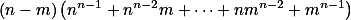 . Teď dokážeme, že tyto dvě závorky jsou nesoudělné. Skutečně
. Teď dokážeme, že tyto dvě závorky jsou nesoudělné. Skutečně 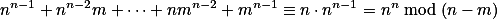 . Proto
. Proto 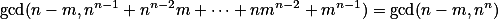 (Eukleidův algoritmus). Pokud by ale nějaké prvočíslo dělilo jak
(Eukleidův algoritmus). Pokud by ale nějaké prvočíslo dělilo jak 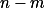 , tak
, tak 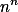 , pak by dělilo i
, pak by dělilo i  a
a 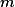 , což je spor s jejich nesoudělností. Tudíž jsou závorky vskutku nesoudělné. Jelikož jejich součin je čtverec, i obě závorky jsou čtverce, tedy skutečně je
, což je spor s jejich nesoudělností. Tudíž jsou závorky vskutku nesoudělné. Jelikož jejich součin je čtverec, i obě závorky jsou čtverce, tedy skutečně je 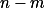 čtverec.
čtverec.
Zadání 16:
V rovině leží několik přímek tak, že každá přímka protíná přesně jiných přímek. V závislosti na
jiných přímek. V závislosti na  určete, kolik přímek může v rovině ležet.
určete, kolik přímek může v rovině ležet.
+ skrytý text
Zadání 16:
V rovině leží několik přímek tak, že každá přímka protíná přesně
Erik Ježek | 27. 5. 2022 20:04:00
Řešení 14:
+ skrytý text
Zadání 15:
Mějme přirozená čísla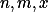 , taková že splňují
, taková že splňují 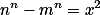 a čísla
a čísla 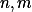 jsou nesoudělná. Dokažte že
jsou nesoudělná. Dokažte že 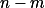 je druhou mocninou přirozeného čísla
je druhou mocninou přirozeného čísla
+ skrytý text
Když za 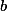 budeme dosazovat čísla od 0 do
budeme dosazovat čísla od 0 do 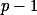 , tak dostaneme
, tak dostaneme  různých zbytků modulo
různých zbytků modulo  , protože: Pro spor předpokládejme, že existují různá celá čísla
, protože: Pro spor předpokládejme, že existují různá celá čísla 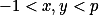 , taková že
, taková že 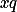 a
a 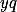 dávají stejný zbytek, pak ale musí platit, že
dávají stejný zbytek, pak ale musí platit, že  dělí
dělí 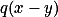 a z toho že
a z toho že  a
a 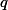 jsou různá prvočísla, tak
jsou různá prvočísla, tak  dělí
dělí 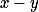 , to ale už znamená
, to ale už znamená 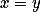 , což je spor. Zbývá ukázat, že každý z těchto zbytků je menší než
, což je spor. Zbývá ukázat, že každý z těchto zbytků je menší než 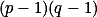 , nebo je prvním větším číslem než tento součin, které dává stejný zbytek modulo
, nebo je prvním větším číslem než tento součin, které dává stejný zbytek modulo  jako
jako 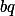 (proto je v následující nerovnosti na levé straně
(proto je v následující nerovnosti na levé straně 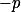 ), pak bude jistě stačit zvolit
), pak bude jistě stačit zvolit  nezáporně pro každé
nezáporně pro každé 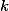 . Podmínku stačí ověřit pro nejvyšší
. Podmínku stačí ověřit pro nejvyšší 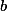 , tedy pro
, tedy pro 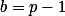 , pak chceme dokázat:
, pak chceme dokázat: 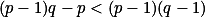 , což ale triviálně platí a tím jsme hotovi
, což ale triviálně platí a tím jsme hotovi
Zadání 15:
Mějme přirozená čísla
Patrik Štencel | 22. 5. 2022 23:33:25
Řešení 13:
+ skrytý text
Zadání 14:
Mějme dvě prvočísla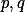 . Dokažme, že pro každé
. Dokažme, že pro každé 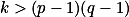 lze
lze 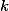 zapsat jako
zapsat jako 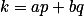 pro nezáporná celá čísla
pro nezáporná celá čísla  .
.
+ skrytý text
Rozdělme si políčka na rohová, okrajová(nepatří do nich rohová) a vnitřní. Rohová mají pouze 2 sousedy, takže nemůže být obarvené. Okrajové má 3 sousedy, takže všichni 3 musí být obarveni. Tabulka je konečná, takže se dostaneme k rohovému políčku, které nemůže být obarvené a tedy ani okrajové nemůže být. Nyní se podívejme na vnitřní políčka. Představme si, že tvoří nějaký mnohoúhelník, kde jeho úhly jsou násobky 90°. Představme si, že nějaký vnitřní úhel má 90°. To by znamenalo, že nějaké políčko má kolem sebe 2 čtverečky. To odporuje zadání, takže jeho jediné vnitřní úhly jsou 180°, 270°,360°(uvnitř). Pokud bychom šli po jeho vnějším obvodu(nepočítáme vnitřní záhyby), mohli bychom sečíst úhly na které narazíme. Pokud bychom brali ty úhly, které nejsou přímé a náš mnohoúhelník by měl n vrcholů, získali bychom tento součet jako n270°. Součet úhlů v mnohoúhelníku je (n-2)180°. Tedy náš útvar nemůže být mnohoúhelník, ale zároveň jediný útvar, který by to mohl být je mnohoúhelník. To je spor a tedy nejde to. (Alternativní metoda by spočívala, že půjdeme po obvodu a vždy budeme zabočovat o 90° na jednu stranu a na druhé straně se bude rozkládat náš obarvený mnohoúhelník. Nyní bychom potřebovali obalit náš mnohoúhelník tím, že uzavřeme jeho obvod. Problém by nastal v tom, že u každého takového uzavření by obarvená část nebyla uvnitř uzavřené části, ale venku(táhla by se do nekonečna/krajů(obojí nejde)).)
Zadání 14:
Mějme dvě prvočísla
Erik Ježek | 22. 5. 2022 20:24:20
Řešení 12:
+ skrytý text
Zadání 13:
Uvažme tabulku s řádky a
řádky a 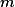 sloupci. Lze tuto tabulku obarvit, tak aby každé obarvené políčko (existuje aspoň jedno) sousedilo s aspoň 3 jinými obarvenými políčky? (Políčko sousedí s jiným políčkem, pokud mají společnou stranu)
sloupci. Lze tuto tabulku obarvit, tak aby každé obarvené políčko (existuje aspoň jedno) sousedilo s aspoň 3 jinými obarvenými políčky? (Políčko sousedí s jiným políčkem, pokud mají společnou stranu)
+ skrytý text
Stačí zvolit 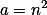 ,
, 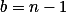 , pak rovnost jistě bude platit a jmenovatel zlomku bude vždy vyšší než 0 (z přirozenosti
, pak rovnost jistě bude platit a jmenovatel zlomku bude vždy vyšší než 0 (z přirozenosti  ).
).
Zadání 13:
Uvažme tabulku s




