Miroslav Olšák | org | 29. 11. 2011 21:10:07
Vejtek: Pro mne to tedy TeMno je, vzdyt ze se bavime 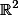 , je zcela nepodstatne, muze to byt cokoli nekonecneho.
, je zcela nepodstatne, muze to byt cokoli nekonecneho.
Anonym | 29. 11. 2011 21:05:53
Štěpán: + skrytý text
Vejtek: + skrytý text
To žádný problém není, protože já si beru pouze nějaké dvojice a je mi úplně jedno jaké. Nemusí (a ani nemůžou) tam být všechny.
Vejtek: + skrytý text
Vybrat si konečný počet nestačí. To nekonečno je tam klíčové.
πtr | org | 29. 11. 2011 20:00:23
Miso: Kružnica "vepsaná" (po slovensky "vpísaná") trojuholníku znamená kružnicu, ktorá má s každou stranou trojuholníka spoločný práve jeden bod, pričom jej stred je vnútri trojuholníka.
Miso z PO | 29. 11. 2011 19:34:42
3 ulohe serialovej v tomto ročniku nechapu pojmu "vepsana". Znamená to vpísana kružnica? Zvonku alebo zvnutra?
Pavel Šalom | 29. 11. 2011 19:23:47
Kuba: Ano, treba tak, jak jsi popsal, se da rozumet tomu, co napsal Tonda.
Vejtek | 29. 11. 2011 18:05:45
Teorie množin se zabývá úlpně jinými problémy [o:
Ad Štěpán:
+ skrytý text
Ad Štěpán:
+ skrytý text
Nepotřebujeme vůbec žádné očíslování. Stačí si pouze dvě dvojice vybrat a ty "porušit" popsaným způsobem. Zbytek se nechá tak.
Co se týče "číslování" obecně, tak lze indexovat libovolnnými množinami (takže i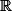 ),
), 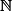 se nám však líbí většinou více pro své "pěkné" vlastnosti (tj. je to spočetné dobré uspořádání), které umožnuje například používat princip indukce. Tahle motivace ihned přinese zobecnění ve formě tzv. ordinálních čísel. Indukce je pak hračka i podle libovolně velkých indexových množin.
se nám však líbí většinou více pro své "pěkné" vlastnosti (tj. je to spočetné dobré uspořádání), které umožnuje například používat princip indukce. Tahle motivace ihned přinese zobecnění ve formě tzv. ordinálních čísel. Indukce je pak hračka i podle libovolně velkých indexových množin.
Co se týče "číslování" obecně, tak lze indexovat libovolnnými množinami (takže i
Kuba | 29. 11. 2011 16:39:49
Moc díky za odpovědi, obě řešení se mi fakt líbí. Ta úloha ale asi není zrovna středoškolská, co? Mě to skoro zavání teorií množin.
+ skrytý text
+ skrytý text
A mám rozumět Tondovu řešení Štěpánovy připomínky anonymova řešení třeba tak, že celou rovinu vyjma bodů [z;0], kde z je celé číslo, zobrazíme ve středové souměrnosti podle počátku a ty vybrané body ve středové souměrnosti kolem bodu [0.5;0]? Nevím jistě, jestli to funguje...
Tonda | 29. 11. 2011 14:08:01
+ skrytý text
Můžeme si vybrat jen nějakou podmnožinu roviny, která obsahuje jen spočetně mnoho těch dvojic.
Štěpán | 29. 11. 2011 13:14:06
Mě by zajímala jedna věc, ohledně posledně zmíněného řešení.
+ skrytý text
+ skrytý text
Není v tomto řešení problém to, že dvojic není spočetně mnoho a tedy si je v podstatě nemůže očíslovat, jak to ve svém řešení dělá? Dá se to případně nějak jednoduše obejít?
Pavel Šalom | 29. 11. 2011 10:32:38
anonym: Samozrejme konstrukci s touto myslenkou je mnoho. Libi se mi, ze tvoje konstrukce je strucna :)
Anonym | 28. 11. 2011 23:27:11
Já bych to cvičení řešil následovně:
+ skrytý text
+ skrytý text
Všimněme si, že otočení o úhel 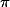 má jediný pevný bod
má jediný pevný bod  . To už nám celou rovinu bez bodu
. To už nám celou rovinu bez bodu  rozdělí na dvojice různých bodů, které se prohazují. Vezměme si tedy nějaké takové dvojice
rozdělí na dvojice různých bodů, které se prohazují. Vezměme si tedy nějaké takové dvojice 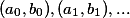 a upravme je na
a upravme je na 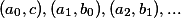 . Tím dostaneme zobrazení, co nemá žádné pevné body.
. Tím dostaneme zobrazení, co nemá žádné pevné body.
Josef Tkadlec | 27. 11. 2011 19:37:26
Nene, autoři mají zobrazení docela podobné.
Smyslem toho cvičení je přesně to, aby si čtenář uvědomil, co všechno je zobrazení. Asi jsme ho (a některá ostatní) měli nějak označit, aby bylo jasné, že je těžké. Pokud by byl zájem, můžeme k (vybraným) cvičením někam napsat aspoň nahrubo napsaná řešení.
Co čokoládové úlohy? Stále nikdo nic? Ani (i)čko toho posledního?
Jinak pilně řešte, první seriálová série se posílá (spolu s Velkými čísly) už za týden!
Smyslem toho cvičení je přesně to, aby si čtenář uvědomil, co všechno je zobrazení. Asi jsme ho (a některá ostatní) měli nějak označit, aby bylo jasné, že je těžké. Pokud by byl zájem, můžeme k (vybraným) cvičením někam napsat aspoň nahrubo napsaná řešení.
Co čokoládové úlohy? Stále nikdo nic? Ani (i)čko toho posledního?
Jinak pilně řešte, první seriálová série se posílá (spolu s Velkými čísly) už za týden!
Pavel Šalom | 27. 11. 2011 18:39:37
Cau Kubo,
ano, jde to i bez nevlastnich bodu. Problem by mohl byt v tom, ze clovek ma tendenci se omezovat na "tradicni" zobrazeni. Kdyz uz opusti tradicni zobrazeni, porad ma tendenci nejak "spojite menit" rovinu, nebo si preje, aby zobrazeni umel zapsat nejakou rovnici. Ale zadna z tech veci neni nutna.
Jak jsem na to prisel:
+ skrytý text
Moje reseni:
+ skrytý text
Autori serialu mozna maji nejake mnohem jednodussi zobrazeni :)
ano, jde to i bez nevlastnich bodu. Problem by mohl byt v tom, ze clovek ma tendenci se omezovat na "tradicni" zobrazeni. Kdyz uz opusti tradicni zobrazeni, porad ma tendenci nejak "spojite menit" rovinu, nebo si preje, aby zobrazeni umel zapsat nejakou rovnici. Ale zadna z tech veci neni nutna.
Jak jsem na to prisel:
+ skrytý text
Zrcadleni dela to, ze body v rovine sparuje do dvojic a potom vlastne rika: v ramci paru prohod body. Bohuzel ale nektere body sparuje samo se sebou.
Moje reseni:
+ skrytý text
Sparuju body treba tak, ze s bodem ![[x,y] [x,y]](https://prase.cz/chat/texmaker.php?tex=%5Bx%2Cy%5D&hash=8d86fd8b5d7133fe3b30) bude v paru bod
bude v paru bod ![[x+1,y] [x+1,y]](https://prase.cz/chat/texmaker.php?tex=%5Bx%2B1%2Cy%5D&hash=2f8f21acffcfc73d62eb) . Musim si ale hlidat, aby kazdy bod byl pouze v jednom paru, tak to popisu trochu podrobneji.
. Musim si ale hlidat, aby kazdy bod byl pouze v jednom paru, tak to popisu trochu podrobneji.
Predstavim si nekonecne pasy sirky 1, ktere si ocisluju celymi cisly. Pas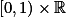 nazvu 1.pasem. Pas
nazvu 1.pasem. Pas 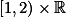 nazvu 2.pasem, atd. Vlevo cisluju podobne: Pas
nazvu 2.pasem, atd. Vlevo cisluju podobne: Pas 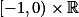 nazvu 0.pasem, pas
nazvu 0.pasem, pas 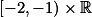 nazvu -1.pasem, atd.
nazvu -1.pasem, atd.
Ted reknu, ze cisla z 1.pasu sparuju s cisly z 2.pasu tak, ze bodu![[x,y] [x,y]](https://prase.cz/chat/texmaker.php?tex=%5Bx%2Cy%5D&hash=8d86fd8b5d7133fe3b30) z 1.pasu priradim bod
z 1.pasu priradim bod ![[x+1,y] [x+1,y]](https://prase.cz/chat/texmaker.php?tex=%5Bx%2B1%2Cy%5D&hash=2f8f21acffcfc73d62eb) z 2.pasu. Podobne 3.pas sparuju se 4.pasem, atd. Stejnetak vlevo -1.pas sparuju s 0.pasem, atd.
z 2.pasu. Podobne 3.pas sparuju se 4.pasem, atd. Stejnetak vlevo -1.pas sparuju s 0.pasem, atd.
Zobrazeni definuju tak, ze prohazuje body, ktere jsou spolu sparovane. Muzu si to teda predstavit tak, ze prohazuje vlastne cele pasy, pricemz vzdy lichy pas posouva o 1 vpravo a sudy pas posouva o 1 vlevo.
Predstavim si nekonecne pasy sirky 1, ktere si ocisluju celymi cisly. Pas
Ted reknu, ze cisla z 1.pasu sparuju s cisly z 2.pasu tak, ze bodu
Zobrazeni definuju tak, ze prohazuje body, ktere jsou spolu sparovane. Muzu si to teda predstavit tak, ze prohazuje vlastne cele pasy, pricemz vzdy lichy pas posouva o 1 vpravo a sudy pas posouva o 1 vlevo.
Autori serialu mozna maji nejake mnohem jednodussi zobrazeni :)
Kuba | 27. 11. 2011 17:29:34
A teď zase já s matematikou o mnoho úrovní nižší a dotazem daleko přízemnějším... Nejsou někde nějaká vzorová řešení cvičení ze seriálu? Přečetl jsem ho celý, ale s pár úlohama vážně nemůžu hnout a rád bych viděl postup. (Přednášku jsem viděl, byla pěkná, bohužel jste tam nedělali nic z toho, co jsem nezvládl.)
Konkrétně mě zajímá jedno z prvních cvičení: "Nalezněte zobrazení, které nemá žádný pevný bod a provedeno dvakrát za sebou je identitou."
Vymyslel jsem jenom příšernosti typu kruhová inverze spojená se středovou souměrností. Jenomže tam si pomáhám nevlastními body. Jde to bez nich?
Předem díky za odpověď.
Konkrétně mě zajímá jedno z prvních cvičení: "Nalezněte zobrazení, které nemá žádný pevný bod a provedeno dvakrát za sebou je identitou."
Vymyslel jsem jenom příšernosti typu kruhová inverze spojená se středovou souměrností. Jenomže tam si pomáhám nevlastními body. Jde to bez nich?
Předem díky za odpověď.
Josef Tkadlec | 25. 11. 2011 18:58:45
Ale kdeže, akorát jsem tu úlohu znal :).
BakyX | 25. 11. 2011 18:00:44
Wow. Však to je viac ako geniálné riešenie. Si génius !!!
Josef Tkadlec | 25. 11. 2011 16:18:25
BakyX: Jelikož už je po termínu, tak je snad OK sem řešení napsat. Je to ale dost dobrá úloha, tak to schovám, ať ostatním řešení úlohy nepokazím ;).
Nejdřív hint:
+ skrytý text
A potom myšlenka řešení:
+ skrytý text
Nejdřív hint:
+ skrytý text
CS!
A potom myšlenka řešení:
+ skrytý text
Cauchyho nerovnost nám dá
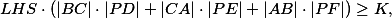
kde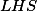 značí levou stranu a
značí levou stranu a 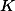 nějakou konstantu nezávislou na poloze bodu
nějakou konstantu nezávislou na poloze bodu  . Velká závorka je ovšem taky konstanta (obsah!), takže si stačí rozmyslet, že rovnost v Cauchym nastává tehdy, je-li
. Velká závorka je ovšem taky konstanta (obsah!), takže si stačí rozmyslet, že rovnost v Cauchym nastává tehdy, je-li  vepsiště
vepsiště 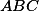 .
.
kde
BakyX | 25. 11. 2011 14:31:14
Pítr: Ďakujem
Pavel: Geogebra je super, program ako stvorený pre niečo ako som ja. To "dementný" som napísal preto, lebo ma fakt nahnevalo, koľko času som strávil nad náčrtom, ktorý som neurobil nakoniec..
Chcem sa ešte spýtať, ako by ste riešili 6. úlohu zo 4. strany http://seminar.strom.sk/priklady/archiv/casop... Ďakujem
Pavel: Geogebra je super, program ako stvorený pre niečo ako som ja. To "dementný" som napísal preto, lebo ma fakt nahnevalo, koľko času som strávil nad náčrtom, ktorý som neurobil nakoniec..
Chcem sa ešte spýtať, ako by ste riešili 6. úlohu zo 4. strany http://seminar.strom.sk/priklady/archiv/casop... Ďakujem
Pavel Šalom | 23. 11. 2011 10:04:47
Cau,
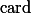 tady bude znamenat pocet prvku. Nevim ale presne, co znamena
tady bude znamenat pocet prvku. Nevim ale presne, co znamena 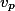 , takze platnost nerovnosti necham na vas.
, takze platnost nerovnosti necham na vas.
Kdyz uz jsme u toho, tak kardinalitu (=mohutnost) bych prelozil jako "zobecnena velikost". Pro konecne mnoziny je to pocet prvku, ale pro nekonecne mnoziny umi kardinalita rozlisovat "velikost nekonecna". Definice na wiki http://cs.wikipedia.org/wiki/Mohutnost.
Napriklad se da ukazat, ze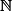 ma mensi kardinalitu nez
ma mensi kardinalitu nez 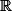 . Muze ale byt prekvapujici, ze
. Muze ale byt prekvapujici, ze 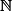 ma stejnou kardinalitu jako
ma stejnou kardinalitu jako 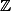 a dokonce jako
a dokonce jako 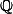 (podrobnosti na wiki nebo na pozadani).
(podrobnosti na wiki nebo na pozadani).
Kdyz uz jsme u toho, tak kardinalitu (=mohutnost) bych prelozil jako "zobecnena velikost". Pro konecne mnoziny je to pocet prvku, ale pro nekonecne mnoziny umi kardinalita rozlisovat "velikost nekonecna". Definice na wiki http://cs.wikipedia.org/wiki/Mohutnost.
Napriklad se da ukazat, ze
Miroslav Olšák | org | 22. 11. 2011 23:27:52
Pravda. Ja mel, nevim proc, pocit, ze tech jednicek vlevo potrebuji jeste o jednu vic.




