BakyX | 14. 11. 2011 14:37:52
Tom: Vyšetril si prípad, keď sú body K, L totožné ? Ja áno..Aj som to pre ten prípad dokázal. A opraveteľ stále našiel chybu !!!
Tom | 14. 11. 2011 12:12:19
Pepa T. no, jak tak koukám, pětadvacítek moc nebude... opravovatel šestky to vzal docela tvrdě... Jsem zvědavej, za co to postrhal, sám ve svym řešení jsem chybu nenašel :D ale aspoň nejsem jedinej...
Josef Tkadlec | 13. 11. 2011 00:10:16
Přednáška k prvnímu dílu seriálu
Slyšte, slyšte! Toto pondělí od 18:00 proběhne v budově MFF v Troji přednáška k prvnímu dílu letošního seriálu. Asi nemusím zdůrazňovat, že to je ideální příležitost, jak se do seriálu pustit :). Všichni jste srdečně zváni.
Pro nepražáky a lenochy mám také dobrou zprávu -- přednáška bude přenášena online! Podrobnosti na http://www.talnet.cz/aktuality.
Slyšte, slyšte! Toto pondělí od 18:00 proběhne v budově MFF v Troji přednáška k prvnímu dílu letošního seriálu. Asi nemusím zdůrazňovat, že to je ideální příležitost, jak se do seriálu pustit :). Všichni jste srdečně zváni.
Pro nepražáky a lenochy mám také dobrou zprávu -- přednáška bude přenášena online! Podrobnosti na http://www.talnet.cz/aktuality.
Josef Tkadlec | 10. 11. 2011 01:22:12
Jestli vážně byla lehká, to se ještě uvidí... Každopádně je tu ještě iKSko (http://kms.sk/iks.php), které se posílá teď v pondělí, tak se do něj všichni pořádně pusťte :).
BakyX | 9. 11. 2011 14:31:44
Pepa T.: Geometrická séria bola neobvykle ľahká..Naschvál znižujete obtiažnosť úloh ? :)
Rado: Skús si dokresliť os nejakej úsečky :) Ale určite sa to dá aj inak.
Rado: Skús si dokresliť os nejakej úsečky :) Ale určite sa to dá aj inak.
Rado | 9. 11. 2011 13:21:10
Ahoj, mě by strašně zajímal nějaký hint do osmičky, mohli byste ho sem dát? Dík moc
Josef Tkadlec | 9. 11. 2011 11:23:47
Ahoj Mišo, proti zákonům PraSete ses nijak neprovinil :-D, na žádnou hloupost se neptáš, úplně chápu tvou zvědavost :). Hint následuje.
+ skrytý text
A co vy ostatní? Jak jste se s úlohami poprali? Byl k něčem úvodní text? Kolik bude pětadvacítek? ;)
+ skrytý text
Možných řešení je víc, nejsnazší je asi dokázat, že součet úhlů u  a
a 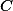 ve čtyřúhelníku
ve čtyřúhelníku 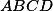 je stejný jako součet úhlů u
je stejný jako součet úhlů u  a
a 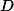 . Pak budou totiž oba součty rovny
. Pak budou totiž oba součty rovny 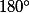 a bude hotovo. Teď je potřeba si označit čtyři dvojice úhlů, které jsou stejné díky odrazům, a dopočítat. Snad to jako náčrt stačí.
a bude hotovo. Teď je potřeba si označit čtyři dvojice úhlů, které jsou stejné díky odrazům, a dopočítat. Snad to jako náčrt stačí.
A co vy ostatní? Jak jste se s úlohami poprali? Byl k něčem úvodní text? Kolik bude pětadvacítek? ;)
Miso | 8. 11. 2011 20:51:58
Vim že to je možne blbé, ale sem slabši v matice jako tu súťažaci. Chtel by sem se spytať, ako som mal dokazať v 4. ulohe ten dôkaz. Je po termine. Dufam, že som sa nespytal nejakou hluposť aneb som se previnil proti zakonom PraSaťa? Stači aspon načrt, nemohu se dočkať rešeni. Vim že to bude v vzoraku ale ja sem nedočkaví. Dekuji.
Vejtek | 7. 11. 2011 15:24:00
Pozor! Nalezena chyba v zadání osmé úlohy čtvrté série. Opravené zadání naleznete v http://mks.mff.cuni.cz/common/show.php?title=...
Miško | org | 4. 11. 2011 14:25:31
Októbrový otvorený problém - Černého hypotéza
Čau, aj keď to bolo bez reakcií, skúsim to uzavrieť :) Ukážem riešenie levelu 1, zvyšok neprezradím.
Problém si predstavme nasledovne: Na papieri máme namaľovaný daný graf, kde políčka sú stavy a z každého vedú dve šípky. Na začiatku postavíme na každé políčko žetón. Vezmime si teraz nejaké synchronizujúce slovo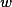 , postupne ho čítajme a s každým prečítaným písmenom posuňme simultánne všetky žetóny po správnej šípke. Keďže
, postupne ho čítajme a s každým prečítaným písmenom posuňme simultánne všetky žetóny po správnej šípke. Keďže 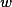 bolo synchronizujúce, na konci skončíme so všetkými žetónmi na jednom políčku.
bolo synchronizujúce, na konci skončíme so všetkými žetónmi na jednom políčku.
Teraz si uvedomme, že nás nezaujíma, koľko žetónov je na ktorom políčku. Podstatné je iba to, ktoré políčka sú obsadené. To znamená, že po prečítaní nejakej časti slova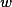 máme
máme 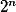 rôznych situácií - každé políčko je buď obsadené, alebo nie. Ak teda
rôznych situácií - každé políčko je buď obsadené, alebo nie. Ak teda 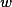 má dĺžku aspoň
má dĺžku aspoň 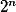 , niektorá situácia sa musela zopakovať. Tým pádom daný úsek slova (medzi týmito dvoma situáciami) môžeme vypustiť a získame tak kratšie synchronizujúce slovo.
, niektorá situácia sa musela zopakovať. Tým pádom daný úsek slova (medzi týmito dvoma situáciami) môžeme vypustiť a získame tak kratšie synchronizujúce slovo.
Ešte doplním, že v súčastnosti je najlepší odhad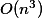 , t.j. taký, ako level 2, akurát s lepšou konštantou. To je o rád horšie než je Černého hypotéza, a keby sa niekomu podarilo tento odhad zlepšiť, bol by to prelom. Takže šanca tam je :)
, t.j. taký, ako level 2, akurát s lepšou konštantou. To je o rád horšie než je Černého hypotéza, a keby sa niekomu podarilo tento odhad zlepšiť, bol by to prelom. Takže šanca tam je :)
Čau, aj keď to bolo bez reakcií, skúsim to uzavrieť :) Ukážem riešenie levelu 1, zvyšok neprezradím.
Problém si predstavme nasledovne: Na papieri máme namaľovaný daný graf, kde políčka sú stavy a z každého vedú dve šípky. Na začiatku postavíme na každé políčko žetón. Vezmime si teraz nejaké synchronizujúce slovo
Teraz si uvedomme, že nás nezaujíma, koľko žetónov je na ktorom políčku. Podstatné je iba to, ktoré políčka sú obsadené. To znamená, že po prečítaní nejakej časti slova
Ešte doplním, že v súčastnosti je najlepší odhad
Kenny | 28. 10. 2011 19:28:03
A ještě pošlu odkaz na další úlohu s Tondovou myšlenkou. Je to Írán 2010!
http://www.artofproblemsolving.com/Forum/view...
http://www.artofproblemsolving.com/Forum/view...
Kenny | 28. 10. 2011 16:24:08
Ahoj,
trochu pohneme s matematickou sekcí.
Pro fanoušky iKSka tu mám jeden příklad, který je velmi podobný úloze A1. Je to nedávný IMO shortlist a určitě si s ním hravě poradíte!
Four real numbers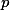 ,
,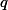 ,
, ,
, satisfy
satisfy 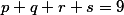 and
and 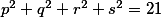 . Prove that there exists a permutation
. Prove that there exists a permutation 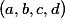 of
of 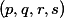 such that
such that 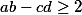 .
.
trochu pohneme s matematickou sekcí.
Pro fanoušky iKSka tu mám jeden příklad, který je velmi podobný úloze A1. Je to nedávný IMO shortlist a určitě si s ním hravě poradíte!
Four real numbers
Kenny | 14. 10. 2011 19:47:46
Ahoj Tondo,
je to pěkná myšlenka. Už jsem ji ale viděl i v úlohách ...
+ skrytý text
je to pěkná myšlenka. Už jsem ji ale viděl i v úlohách ...
+ skrytý text
Balkan 2010 úloha 1 http://www.artofproblemsolving.com/Forum/reso...
USAMO 1993 - úloha 2
http://www.artofproblemsolving.com/Forum/reso...
Určitě ji tam najdeš nejen ty, ale i ostatní :)
USAMO 1993 - úloha 2
http://www.artofproblemsolving.com/Forum/reso...
Určitě ji tam najdeš nejen ty, ale i ostatní :)
Tonda | 14. 10. 2011 00:30:25
takže to je část a), část b) zní: dokažte, že dvě zmíněné kružnice se splývají.
Tonda | 13. 10. 2011 18:16:31
Ahoj,
Zkuste geometrickou úlohu, kterou jsem vymyslel já.
Mějme tětivový čtyřúhelník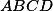 ,
, 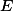 je průsečík přímek
je průsečík přímek 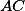 a
a 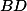 . Dále nechť
. Dále nechť 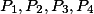 jsou paty kolmic z E na přímky
jsou paty kolmic z E na přímky 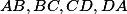 a
a 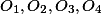 jsou středy kružnic opsaných trojúhelníkům
jsou středy kružnic opsaných trojúhelníkům 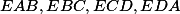 . Dokažte, že
. Dokažte, že 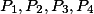 leží na jedné kružnici právě tehdy, když
leží na jedné kružnici právě tehdy, když 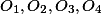 leží na jedné kružnici.
leží na jedné kružnici.
Zkuste geometrickou úlohu, kterou jsem vymyslel já.
Mějme tětivový čtyřúhelník
Miško | org | 5. 10. 2011 22:29:37
Chybicka sa vludila, ma to byt +1 a nie -1, opravim...
šnEk | 5. 10. 2011 21:57:54
Ten odhad v levelu 2 nefunguje pro n < 4, nechybí tam nějakej předpoklad o velikosti n?
Šavlík | org | 5. 10. 2011 20:35:48
aha, tak to jsem špatně pochopil úlohu. Myslel jsem, že z každého stavu se musím dostat zpátky na to samé místo...
Miško | org | 5. 10. 2011 20:23:12
Prázdne slovo sa pripúšťa, ale samozrejme nie je synchronizujúce, pretože každý stav skončí tam, kde začal (t.j. ani náhodou sa nespoja do jedného).
Šavlík | org | 5. 10. 2011 18:14:34
ještě s dovolením přidám level pro sraby :-)
Level 0: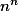
jsem na levelu 0!
(předpokládám ale, že prázdná slova se nepočítají :-))
Level 0:
jsem na levelu 0!
(předpokládám ale, že prázdná slova se nepočítají :-))




