Miško | org | 5. 10. 2011 17:41:35
Októbrový otvorený problém - Černého hypotéza
Je zaujímavé, koľko je v matematike otvorených problémov s jednoduchým zadaním, ktoré môže pochopiť (a možno aj vyriešiť :)) aj stredoškolák. Jedným z nich je aj Černého hypotéza, tu ukážem jednu verziu zadania.
Najprv definujeme automat. To bude orientovaný graf so sľučkami. Bude mať vrcholov, ktoré budeme nazývať stavmi a z každého stavu budú vychádzať dve šípky do nejakého iného alebo aj rovnakého stavu, pričom jedna bude ozačená
vrcholov, ktoré budeme nazývať stavmi a z každého stavu budú vychádzať dve šípky do nejakého iného alebo aj rovnakého stavu, pričom jedna bude ozačená  a druhá
a druhá 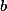 . Keď nám teraz niekto zadá počiatočný stav a slovo z písmen
. Keď nám teraz niekto zadá počiatočný stav a slovo z písmen  a
a 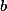 , môžeme postupne čítať písmená a posúvať sa príslušnými šípkami, až na konci zase skončíme v nejakom stave.
, môžeme postupne čítať písmená a posúvať sa príslušnými šípkami, až na konci zase skončíme v nejakom stave.
Slovo nazveme synchronizujúce, ak nezávisle na voľbe počiatočného stavu po jeho prečítaní skončíme vždy v jednom danom stave. Nuž a Černého hypotéza znie:
Ak má -stavový automat synchronizujúce slovo, tak má synchronizujúce slovo dĺžky nanajvýš
-stavový automat synchronizujúce slovo, tak má synchronizujúce slovo dĺžky nanajvýš 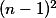 .
.
Zatiaľ neprezradím, aký je najlepší dokázaný odhad, dám vám ale nejaké návodné úlohy... Nezabudnite vaše riešenia napísať na chat a pochváliť sa s levelom!
==============================
Level 1: Dokážte odhad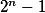 .
.
Level 2: Dokážte odhad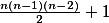 . Hint: + skrytý text
. Hint: + skrytý text -stavový automat, ktorého minimálne synchronizujúce slovo má dĺžku
-stavový automat, ktorého minimálne synchronizujúce slovo má dĺžku 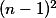 .
.
Je zaujímavé, koľko je v matematike otvorených problémov s jednoduchým zadaním, ktoré môže pochopiť (a možno aj vyriešiť :)) aj stredoškolák. Jedným z nich je aj Černého hypotéza, tu ukážem jednu verziu zadania.
Najprv definujeme automat. To bude orientovaný graf so sľučkami. Bude mať
Slovo nazveme synchronizujúce, ak nezávisle na voľbe počiatočného stavu po jeho prečítaní skončíme vždy v jednom danom stave. Nuž a Černého hypotéza znie:
Ak má
Zatiaľ neprezradím, aký je najlepší dokázaný odhad, dám vám ale nejaké návodné úlohy... Nezabudnite vaše riešenia napísať na chat a pochváliť sa s levelom!
==============================
Level 1: Dokážte odhad
Level 2: Dokážte odhad
Aké krátke môže byť slovo, ktoré spojí dva stavy do jedného?
Level 3: Nájdite Kenny | 4. 10. 2011 11:07:14
K úloze od BakyX. Esence problému se skrývá v následujícím tvrzení
+ skrytý text
+ skrytý text
Jacobi's theorem:
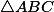 . Najdeme body
. Najdeme body 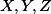 tak, že
tak, že 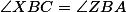 ,
, 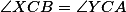 ,
, 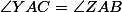 .
.
Pak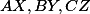 procházejí jedním bodem.
procházejí jedním bodem.
Důkaz tvrzení pomocí goniometrického tvaru Cevovy věty jistě zvládnete, stejně jako jeho aplikaci pro trojúhelník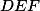 v zadané úloze.
v zadané úloze.
Pak
Důkaz tvrzení pomocí goniometrického tvaru Cevovy věty jistě zvládnete, stejně jako jeho aplikaci pro trojúhelník
BakyX | 30. 9. 2011 00:07:51
Ja som si to všimol. A aj to, že s nimi to každý vyrieši :)
Josef Tkadlec | 29. 9. 2011 18:32:51
Fííha... To jste si všimli, že na stránkách olympiády (http://www.math.muni.cz/~rvmo/) se objevily návodné a doplňující úlohy k domácímu kolu?
Josef Tkadlec | 27. 9. 2011 14:26:43
Jinak koukám, že nám tady ještě zbyla jedna otevřená úloha od BakyXe z konce července. A je to geometrie, to je potřeba podporovat!
V ostrojuholnom trojuholníku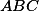 označme
označme 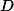 ,
, 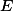 ,
, 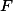 päty výšok na strany
päty výšok na strany  ,
, 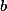 ,
,  . Označme
. Označme 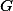 ,
, 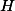 ,
, 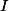 stredy kružníc vpísanych trojuholníkom
stredy kružníc vpísanych trojuholníkom 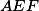 ,
, 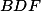 ,
, 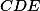 . Dokáž, že priamky
. Dokáž, že priamky 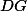 ,
, 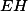 ,
, 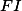 prechádzajú jedným bodom.
prechádzajú jedným bodom.
Následuje řešení. Není zrovna rychlé, ale zato je poměrně standardní a poučné, byť vyžaduje trochu pokročilejší nástoroje. Jestli někdo máte nějaké elementárnější řešení, sem s ním!
+ skrytý text
V ostrojuholnom trojuholníku
Následuje řešení. Není zrovna rychlé, ale zato je poměrně standardní a poučné, byť vyžaduje trochu pokročilejší nástoroje. Jestli někdo máte nějaké elementárnější řešení, sem s ním!
+ skrytý text
Kresli si obrázek :). Chceme dokázat, že v trojúhelníku 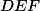 se přímky
se přímky 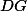 ,
, 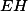 a
a 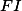 protínají v jednom bodě. Na to je "známé" kritérium -- jmenuje se Cevova věta (viz http://en.wikipedia.org/wiki/Ceva's_theorem). My použijeme její trigonometrickou verzi. Stačí tedy ukázat, že
protínají v jednom bodě. Na to je "známé" kritérium -- jmenuje se Cevova věta (viz http://en.wikipedia.org/wiki/Ceva's_theorem). My použijeme její trigonometrickou verzi. Stačí tedy ukázat, že
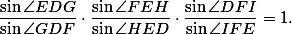
Úhly, jejichž siny ve vztahu vystupují, jsou dost nepříjemné, zkusme se jich proto zbavit. Použitím sinové věty pro trojúhelník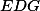 máme
máme
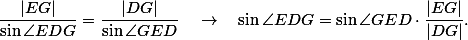
Představme si teď, že podobnými výrazy nahradíme všechny siny v dokazovaném vztahu. Chceme říct, že se na jeho levé straně všechno pokrátí a opravdu dostaneme jedničku.
Délky hlavních úhlopříček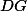 ,
, 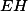 ,
, 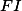 se pokrátí, protože každá z nich bude vystupovat jednou v čitateli a jednou ve jmenovateli. Podobně se pokrátí siny úhlů, neboť
se pokrátí, protože každá z nich bude vystupovat jednou v čitateli a jednou ve jmenovateli. Podobně se pokrátí siny úhlů, neboť 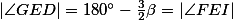 (rozmysli si :) ). Zbývá dokázat, že
(rozmysli si :) ). Zbývá dokázat, že
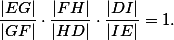
Povšimněme si, že trojúhelníky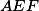 ,
, 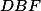 a
a 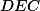 jsou všechny podobné trojúhelníku
jsou všechny podobné trojúhelníku 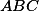 (s vrcholy v tomto pořadí). Označíme-li
(s vrcholy v tomto pořadí). Označíme-li 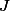 střed kružnice vepsané celému trojúhelníku
střed kružnice vepsané celému trojúhelníku 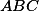 , můžeme díky těmto podobnostem psát
, můžeme díky těmto podobnostem psát
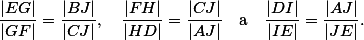
Vynásobením těchto tří vztahů jsme hotovi. Byla to fuška, ale máme to :).
Úhly, jejichž siny ve vztahu vystupují, jsou dost nepříjemné, zkusme se jich proto zbavit. Použitím sinové věty pro trojúhelník
Představme si teď, že podobnými výrazy nahradíme všechny siny v dokazovaném vztahu. Chceme říct, že se na jeho levé straně všechno pokrátí a opravdu dostaneme jedničku.
Délky hlavních úhlopříček
Povšimněme si, že trojúhelníky
Vynásobením těchto tří vztahů jsme hotovi. Byla to fuška, ale máme to :).
Šavlík | org | 25. 9. 2011 15:02:06
Pavel: Střídají se po jednom podání.
Pavel Šalom | 25. 9. 2011 14:50:21
Co znamená pravidelné střídání podání? Znamená to, že se střídají přesně po jednom podání, nebo to znamená, že se mohou střídat třeba vždy po třech podáních?
Josef Tkadlec | 25. 9. 2011 01:01:06
Tak to abychom ji využili! :) Neváhejte sem (schovaně) psát nápady, dílčí řešení, komentáře nebo vlastně cokoliv k následující úloze:
Dva hráči (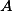 a
a 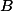 ) hrají proti sobě něco jako tenis. Oba mají nějakou (ne nutně stejnou) pevnou šanci na to, že míček, který sami podávají, vyhrajou. Kdo první vyhraje
) hrají proti sobě něco jako tenis. Oba mají nějakou (ne nutně stejnou) pevnou šanci na to, že míček, který sami podávají, vyhrajou. Kdo první vyhraje  míčků, vyhrává celkově. Podání se střídá podle jednoho ze dvou schémat: Buď pravidelně, nebo vždycky podává ten, kdo vyhrál minulý míček (vždy začíná podávat
míčků, vyhrává celkově. Podání se střídá podle jednoho ze dvou schémat: Buď pravidelně, nebo vždycky podává ten, kdo vyhrál minulý míček (vždy začíná podávat 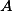 ).
).
Dokažte, že šance hráčů na celkovou výhru nezávisí na volbě schématu.
Dva hráči (
Dokažte, že šance hráčů na celkovou výhru nezávisí na volbě schématu.
Miško | org | 24. 9. 2011 13:20:30
Ahoj, máme pre vás novú feature:
+ skrytý text
+ skrytý text
Šavlík pre vás naprogramoval skrývanie textu!
Josef Tkadlec | 20. 9. 2011 21:50:16
Že jsem se ale musel snažit... A co, bolelo to? :D
Martin Čech | 20. 9. 2011 21:34:48
Pepa mě donutil, abych sem napsal, že jsem to vyřešil bez hintu, a že to čtvrté číslo je 164. Jsou to jediná trojciferná čísla s různými ciframi, která když zapíšeme v desítkovém zápisu ve tvaru ABC, tak platí, že A*BC=C*AB.
Miroslav Olšák | org | 20. 9. 2011 14:04:00
Dobra, tak s hintem uz jsem Pepovu trojcifernou hricku vyresil. Kdo dal?
Zbyněk | 15. 9. 2011 17:18:47
@Pepa: docela zajímavý, že se z té české olympiády dostala do sbírky PEN (stojí za stáhnutí)
http://www.artofproblemsolving.com/Forum/view...
http://www.artofproblemsolving.com/Forum/view...
Josef Tkadlec | 15. 9. 2011 12:36:55
Hrál jsem si tak jednou s trojcifernými čísly, která mají všechny cifry různé, a napadla mě zajímavá vlastnost, kterou by taková čísla mohla mít. Po chvilce počítání jsem zjistil, že existují přesně čtyři čísla s touto vlastností (trojciferná s různými ciframi). Tři z nich jsou 195, 265 a 498. Co je to za vlastnost? Které číslo je to čtvrté? :)
P.S. Předchozí úloha byla (věřte nevěřte) z archivu české matematické olympiády. Můžete se o tom přesvědčit na http://cgi.math.muni.cz/~rvmo/ABC/48/A48s.pdf.
P.S. Předchozí úloha byla (věřte nevěřte) z archivu české matematické olympiády. Můžete se o tom přesvědčit na http://cgi.math.muni.cz/~rvmo/ABC/48/A48s.pdf.
Josef Tkadlec | 9. 9. 2011 15:03:29
Našel jsem dobrou legrácku, tak se musím podělit. Schválně si zkuste, není těžká. A můžete taky tipovat zdroj :).
Ukažte, že pro každé přirozené číslo je hodnota součinu
je hodnota součinu
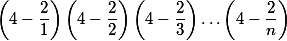
celočíselná.
Ukažte, že pro každé přirozené číslo
celočíselná.
Josef Tkadlec | 5. 9. 2011 18:14:36
Na stránkách http://skmo.sk už je k vidění zadání aktuálního MEMa. A kdo že tam mimo jiné zadal úlohu...? Miško! :)
Miško | org | 30. 8. 2011 22:22:02
Tak už funguje aj TeX vložený do jedného alebo dvoch dolárov, dokonca je rozdiel medzi riadkovým 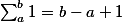 a odstavcovým TeXom:
a odstavcovým TeXom:
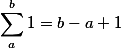
BakyX | 30. 7. 2011 23:47:25
Ďakujem.
šnEk | 29. 7. 2011 00:56:23
BakyX: Já jsem ti nakonec zapomněl odpovědět. V seriálu je jedna podobná rovnice vyřešená, podívej se na úlohu na straně 41 letošního seriálu: http://mks.mff.cuni.cz/common/show.php?title=...
V zásadě jde o to, pravou stranu rozložit na Gaussova prvočísla a levou do tvaru (a+ib)(a-ib). Pak už to půjde snadno.
Jinak Gaussova prvočísla jde samozřejmě i objejít, jedna z těch snazších možností je zkusit rovnici ještě převést do hezčího tvaru
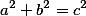 ,
,
tohle řešení se dá najít třeba v archivech olympiády http://cgi.math.muni.cz/~rvmo/ABC/55/A55i.pdf.
Druhá možnost je uhodnout řešení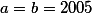 a použít geometrickou metodu z posledního dílu předloňského seriálu.
a použít geometrickou metodu z posledního dílu předloňského seriálu.
Žádný z těch řešení není nic moc extra, ale poprat se s tím dá.
V zásadě jde o to, pravou stranu rozložit na Gaussova prvočísla a levou do tvaru (a+ib)(a-ib). Pak už to půjde snadno.
Jinak Gaussova prvočísla jde samozřejmě i objejít, jedna z těch snazších možností je zkusit rovnici ještě převést do hezčího tvaru
tohle řešení se dá najít třeba v archivech olympiády http://cgi.math.muni.cz/~rvmo/ABC/55/A55i.pdf.
Druhá možnost je uhodnout řešení
Žádný z těch řešení není nic moc extra, ale poprat se s tím dá.
anonym | 28. 7. 2011 21:12:41
ahoj dokazali byste nebo vyvratili tudle nerovnost pro vsechny cely cisla vetsi nez 1 000 000 http://www.wolframalpha.com/input/?_=13117999...




